http://en.wikipedia.org/wiki/Division_%28digital%29
I'm trying to divide some extremely large numbers using a Newton-Raphson iteration.
It's good because division is a linear function: (leaving out a remainder or decimal for now)
a small # eg: 987987/123
N/D = Q
987987/123 = Q
987987=123Q
f(X) = 123Q-987987
look familiar? y=mX+b
... which means that the numerator is just the Y intercept, the denominator(divisor) is the slope(delta), and the '0' of the function is the answer of the division problem.
Newton-Raphson states that with an initial guess of X(i), you gain precision by calculating X(i+1), X(i+2), .... with the following formula:
X(i+1) = X(i) - [ (f(X(i)) / delta X]
with delta X just being the denominator (slope)
eg: 987987/123 (actual answer of 8032.41463)
(guess) X(i) = 7500
iteration1 = X(i+1) = 7500 - {[123(7500) - 987987] / 123} = 6967.58537
iteration2 = x(i+1) = 6967.58537 - {[123(6967.58537) - 987987] / 123} = 8032.41463
Two iterations!
My problem is the other part of the equation, in which the reciprocal of the slope(delta or secant) of the function is solved for in order to complete the formula using only multiplication, subtraction, and addition algorithms:
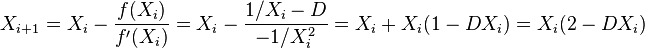
for which I have substituted numbers into many different ways and can not make a reciprocal out of it. Have any fellow math/CS geeks in here dealt with this problem before?
Thanks
I'm trying to divide some extremely large numbers using a Newton-Raphson iteration.
It's good because division is a linear function: (leaving out a remainder or decimal for now)
a small # eg: 987987/123
N/D = Q
987987/123 = Q
987987=123Q
f(X) = 123Q-987987
look familiar? y=mX+b
... which means that the numerator is just the Y intercept, the denominator(divisor) is the slope(delta), and the '0' of the function is the answer of the division problem.
Newton-Raphson states that with an initial guess of X(i), you gain precision by calculating X(i+1), X(i+2), .... with the following formula:
X(i+1) = X(i) - [ (f(X(i)) / delta X]
with delta X just being the denominator (slope)
eg: 987987/123 (actual answer of 8032.41463)
(guess) X(i) = 7500
iteration1 = X(i+1) = 7500 - {[123(7500) - 987987] / 123} = 6967.58537
iteration2 = x(i+1) = 6967.58537 - {[123(6967.58537) - 987987] / 123} = 8032.41463
Two iterations!
My problem is the other part of the equation, in which the reciprocal of the slope(delta or secant) of the function is solved for in order to complete the formula using only multiplication, subtraction, and addition algorithms:
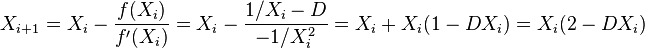
for which I have substituted numbers into many different ways and can not make a reciprocal out of it. Have any fellow math/CS geeks in here dealt with this problem before?
Thanks


