You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
DSP Whodunnit.
- Thread starter chmedly
- Start date
Help Support GroupDIY Audio Forum:
This site may earn a commission from merchant affiliate
links, including eBay, Amazon, and others.
mskeete said:I missed the duplicate numbers when I looked earlier. Will take another look at the examples.
Do you have input / output gain control settings?
It may have only been the No Filters situation that had matching coefficients. A couple of the ones with filters that I just looked at did not appear to have any matching numbers. :-\
mskeete said:Do you have input / output gain control settings?
I'm not sure what you're asking. There are a number of gain stages in the signal path in these devices and they are controlled via documented commands. There IS a documented command set for these units and most of the parameters are available with them. The EQ is not documented which is why I'm trying to decode it. I have deduced a few other non-documented commands but the EQ is a more complicated scheme. Does this answer it?
On the topic of Bandwidth, I have some more examples:
1Khz parametric bandwidth = 1.0 -4db
0102FC00E803F304B53F
1Khz parametric bandwidth = 0.49 -4db
0102FC00E80377BE3740
1Khz parametric bandwidth = 0.2 -4db
0102FC00E8037FA5E640
1Khz parametric bandwidth = 0.1 -4db
0102FC00E803B5CB5141
1Khz parametric bandwidth = 10 +4db
0102FC00E8030820003D
670Hz Band Pass Bandwidth = 2.54
060100009E020000003F
670Hz Band Pass Bandwidth = 5.99
060100009E022108023E
670Hz Band Pass Bandwidth = 10
060100009E020820003D
mskeete said:if you use the formula on the Rane note page to convert from bandwidth to Q them the numbers work out close enough .
IEEE754_Q=SQRT(POWER(2,bandwidth)) / (POWER(2,bandwidth)-1)
Awesome! Thanks for your help.
I had to divert my attention away from this for the past week but I'm still hoping to figure it out. I tried converting to double precision coefficients but that doesn't seem to work either. I'm starting to feel stuck and might post on the stackexchange dsp forum to see if some bright folks there have any ideas.
OK, I thought you had given up or silently cracked it 
So, for the 68 byte data, what would be nice is a set of data dumps with just one filter turned on and only one parameter changed say 10 times.
e.g LPF, butterworh , 100hz, 200hz, ...10khz
So, for the 68 byte data, what would be nice is a set of data dumps with just one filter turned on and only one parameter changed say 10 times.
e.g LPF, butterworh , 100hz, 200hz, ...10khz
Naw. I'd let you know if I cracked it. And I'm not sure I'm ever really willing to admit I've given up. :-[mskeete said:OK, I thought you had given up or silently cracked it
I posted about this on the Stackexchange Reverse Engineering category (in beta I guess). I got a comment there that the 17 coefficients line up with the (3) sets of 5 plus (2) gain multipliers that you would expect with 3 cascaded biquads. They also suggested that I try changing one byte at a time and watch the change in response to a signal going through. Seeing how the first 2 words appear to behave a little different from the rest I'm inclined to try some experimentation by changing one of those values and watching the response. https://reverseengineering.stackexchange.com/questions/17238/decode-filter-coefficients-for-audio-dsp?noredirect=1#comment27098_17238
So, for the 68 byte data, what would be nice is a set of data dumps with just one filter turned on and only one parameter changed say 10 times.
Well, I have this. It's a first order highpass filter at different frequencies.
Code:
100hz:
755DCE3B000000001F03A83E12A95F3F54CAF8BE7BAB5C3FADC5013FC44BAA3EB9A98E3BFBFD7FBF96AA0EBBD8FF7F3FA777AA3E738D5DBF354200BFF7C65DBFB6BDFF3E
120hz:
39C8F53B000000008582A73EC305603F1C5AF7BE30775C3F701E023FE238AA3E921EAB3B18FD7FBF10202BBBC7FF7F3F776DAA3EC0855DBF6A4F00BFC8CA5DBF77B0FF3E
150hz:
0AE8173C00000000EDC5A63E408C603F8832F5BE1B295C3F62A2023FA01CAA3E85C1D53B78FB7FBF6EC455BBA7FF7F3F325EAA3E317A5DBF336300BF81D05DBF9D9CFF3E
180hz:
C548343C00000000580EA63E610D613FF80BF3BE73DB5B3FEA24033F7200AA3ECC2A003C7BF97FBF4F2D80BB80FF7F3FF04EAA3E9E6E5DBFF67600BF38D65DBFC588FF3E
220hz:
782A593C000000001421A53E67B1613FA92FF0BE90745B3FCED0033FFCDAA93EDD811C3C48F67FBF6F869CBB41FF7F3F9C3AAA3E295F5DBF449100BFD5DD5DBF546EFF3E
260hz:
AAFF7C3C000000000D3CA43E5C4C623FA055EDBE6A0E5B3F497A043FA8B5A93E83CB383C73F27FBF09D3B8BBF5FE7F3F4D26AA3EAE4F5DBF87AB00BF6FE55DBFE853FF3E
320hz:
6770983C000000002DF3A23E5924633F5A13E9BE91765A3F1D74053FEB7DA93E9520633C87EB7FBF8F2EE3BB6DFE7F3FE107AA3E68385DBFD5D200BFD2F05DBF4F2CFF3E
400hz:
4563B93C000000005756A13EE626643FBC6FE3BE9EAE593F4CB9063F1234A93E04B18D3C1FE07FBF98BE0DBC8CFD7F3F62DFA93E49195DBF150701BFF8FF5DBF94F7FE3E
500Hz:
9526E03C0000000033789F3E673D653F9A75DCBEA4B8583F9B43083F84D8A83ECAB2B03C68CE7FBF23CD30BC2FFC7F3FDFACA93E3BF25CBF264801BFDA125EBFC3B5FE3E
600Hz:
3F3B023D0000000052C09D3E6E25663F5692D5BEF2C6573F15C1093FCD7DA83E5A88D33CE5B87FBF98B553BC87FA7F3F7A7AA93E01CB5CBFF18801BFAF255EBF0D74FE3E
720Hz:
938F163D00000000DCDD9B3EFA02673FA76FCDBE69AA563FDD7A0B3F0D12A83E081AFD3C249A7FBF9C677DBC29F87F3F253EA93EB59B5CBF58D601BF353C5EBF5425FE3EOk, here's a few "wiggles" of the coefficients:
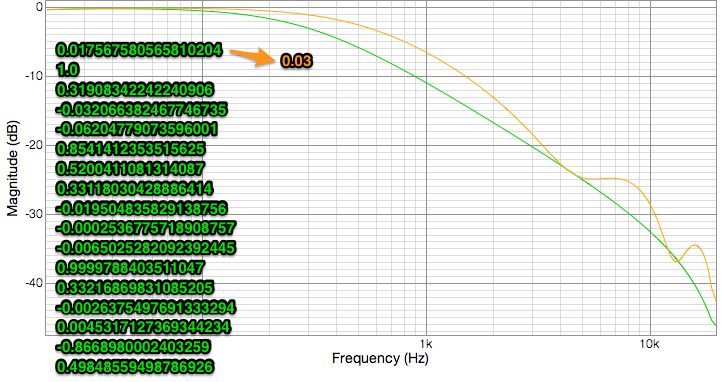
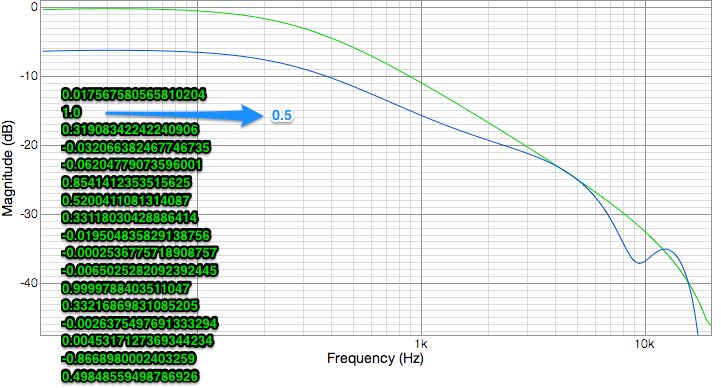
If I change this 2nd coefficient to 2.0, I get the exact same response as 1.0.
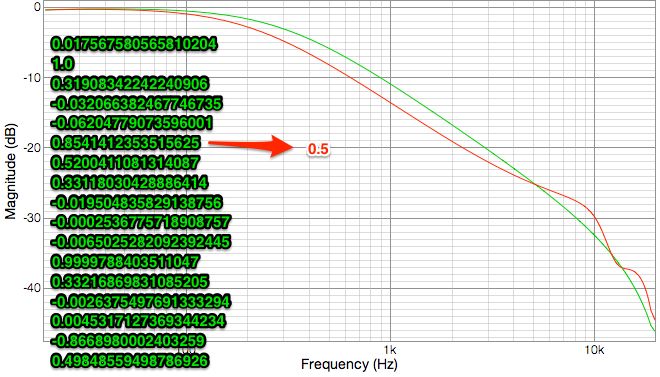
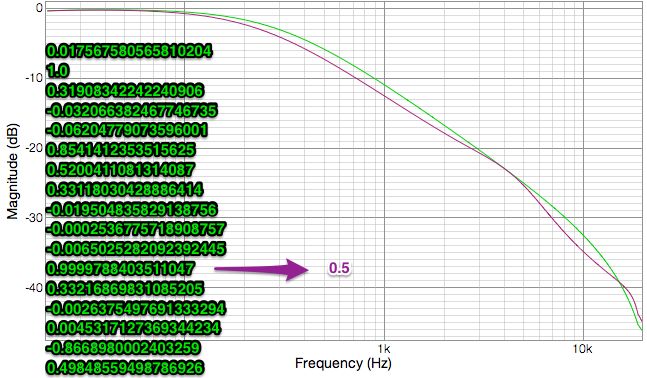
Interestingly, when I tried to change the 7th coefficient (0.5200....) to 1.0 it locked the box up. Then I tried changing it to .999 and it locked it up again.


If I change this 2nd coefficient to 2.0, I get the exact same response as 1.0.


Interestingly, when I tried to change the 7th coefficient (0.5200....) to 1.0 it locked the box up. Then I tried changing it to .999 and it locked it up again.
These graphs are my measurements of the unit. The green trace corresponds to the green list of coefficients. These are the coefficients that the software created for a 300Hz 1st order low pass filter. The alternate color trace is what happens when I change the one coefficient indicated.
Following are the HEX for 2nd order butterworth high pass filters: (I hope 5hz increments are ok)
Following are the HEX for 2nd order butterworth high pass filters: (I hope 5hz increments are ok)
Code:
100Hz:
FF38943B00000000282C4B3EEEC97D3F013A043ED40B7F3F779FB03D47B7CB3E23EAA13EA7DC72BF10BF9B3E4CDE733FC261CC3E48D64EBF83D816BFF2494FBF6A39163F
105Hz:
4D759B3B000000005A184B3E99AC7D3FF07D073E8BFF7E3FF100B53D93A9CB3E2619A23ED0D472BF979F9B3E52E3733F6B5CCC3ED0D24EBF45DD16BF404C4FBF3C36163F
110Hz:
6EADA23B00000000A5044B3E2C8F7D3F22AE0A3E40F37E3F5748B93DE39BCB3E2148A23EF8CC72BF21809B3E56E8733F1457CC3E58CF4EBF06E216BF8D4E4FBF0F33163F
115Hz:
67E1A93B0000000008F14A3EA7717D3FE8CB0D3EF3E67E3F6D77BD3D388ECB3E1577A23E1EC572BFAF609B3E58ED733FBE51CC3EE0CB4EBFC8E616BFDB504FBFE12F163F
120Hz:
3C11B13B0000000083DD4A3E0A547D3F71D8103EA4DA7E3FC68FC13D9180CB3E01A6A23E43BD72BF40419B3E59F2733F694CCC3E67C84EBF88EB16BF28534FBFB42C163F
125Hz:
EF3CB83B0000000017CA4A3E54367D3FCCD4133E53CE7E3FCA92C53DEE72CB3EE5D4A23E67B572BFD4219B3E59F7733F1347CC3EEFC44EBF49F016BF75554FBF8629163F
130Hz:
8664BF3B00000000C3B64A3E87187D3FEEC1163E00C27E3FC081C93D4E65CB3EC203A33E89AD72BF6C029B3E56FC733FBE41CC3E77C14EBF09F516BFC2574FBF5926163F
135Hz:
0288C63B0000000087A34A3EA1FA7C3FB2A0193EACB57E3FCD5DCD3DB357CB3E9732A33EABA572BF07E39A3E5201743F693CCC3E00BE4EBFC9F916BF0F5A4FBF2C23163F
140Hz:
69A7CD3B0000000062904A3EA5DC7C3FE2711C3E56A97E3FFE27D13D1C4ACB3E6461A33ECB9D72BFA6C39A3E4C06743F1537CC3E88BA4EBF89FE16BF5B5C4FBFFF1F163F
145Hz:
BEC2D43B00000000567D4A3E90BE7C3F34361F3EFE9C7E3F45E1D43D893CCB3E2A90A33EEA9572BF48A49A3E450B743FC131CC3E10B74EBF480317BFA85E4FBFD31C163F
150Hz:
03DADB3B00000000616A4A3E64A07C3F4FEE213EA4907E3F818AD83DFB2ECB3EE9BEA33E078E72BFEE849A3E3C10743F6D2CCC3E98B34EBF070817BFF4604FBFA619163FSimilar threads
- Replies
- 6
- Views
- 1K


