dmnieto
Well-known member
You need to apply some windowing and pre-processing in order to transform that into a frequency response that you can read. A simple FFT would not do it...
dmnieto said:You need to apply some windowing and pre-processing in order to transform that into a frequency response that you can read. A simple FFT would not do it...
[y, Fs, nbits] = wavread('testfile');
T = 1/Fs;
L = length(y);
t = (0:L-1)*T;
plot(Fs*t,y);
NFFT = 2^nextpow2(L);
Y = fft(y,NFFT)/L;
f = Fs/2*linspace(0,1,NFFT/2+1);
plot(f,2*abs(Y(1:NFFT/2+1)));culteousness1 said:Hi Ian,
finally, I found some time to test with MATLAB.
Totally forgot about the window size et al.
Here are 9 lines that basically come from
MATLAB's documentation:
I would suggest to test with small parts of your audio file first.Code:[y, Fs, nbits] = wavread('testfile'); T = 1/Fs; L = length(y); t = (0:L-1)*T; plot(Fs*t,y); NFFT = 2^nextpow2(L); Y = fft(y,NFFT)/L; f = Fs/2*linspace(0,1,NFFT/2+1); plot(f,2*abs(Y(1:NFFT/2+1)));
The lines 1 - 5 should give you a plot of the audio.
Maybe some adoption for correct SCILAB syntax as needed.
Cheers,
Carsten
dmnieto said:The wav he has is the output of the chirp function through the EQ, so unless he manages to find the original wav or the formula that generated the chirp it will not work very well. I expect is to be either a discrete or continuous log or linear chirp. A plot of the wav in the time domain will help a lot to determine what the signal was
ruffrecords said:The original sweep was made using Protools. It was done by another group member who has a 2-610 and kindly agreed to do it for ,e. I am not a Protools user so I have no idea what sweep options it has available.
Cheers
Ian
dmnieto said:Let's do something, upload the wav somewhere and I will do the processing for you. Then I will share the code. I would like to play with the data to see how to infer the frequency response.
dmnieto said:Hi Ian,
Good news is that it is a pure chirp, so a simple envelope detection is going to be able to recover all the band.
Bad news is that it is a *linear* chip... so resolution in the low frequencies is going to suck as there is just not enough datapoints to get a frequency response without quite a lot of aliasing.
It is always better to do the analysis in a log chirp but I'll do what I can
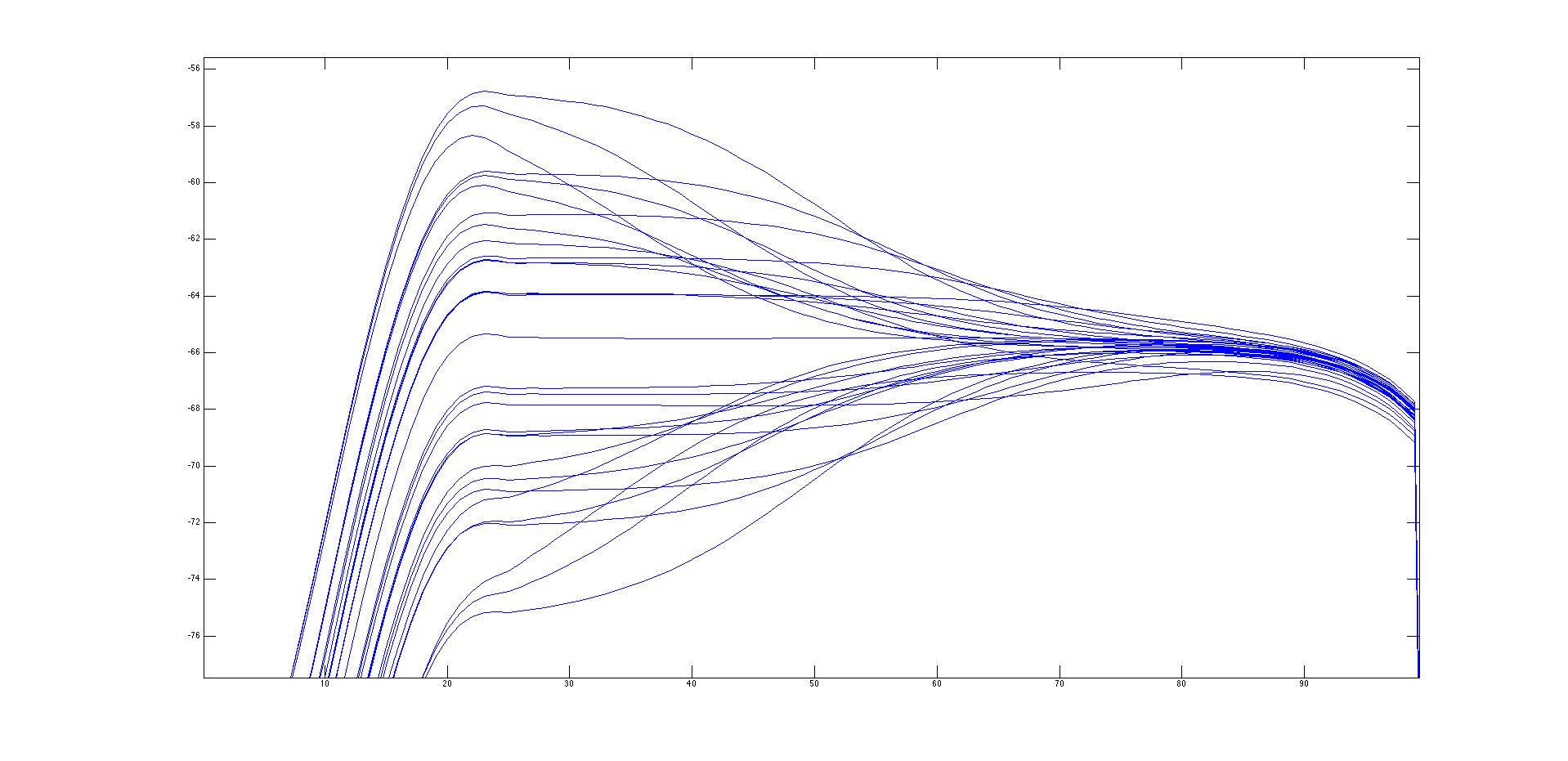
dmnieto said:So Ian, sorry that it took me some time. I have started to do the analysis... and as I expected there is not enough data to make an accurate estimation of anywhere lower that 70Hz... I cannot differentiate if the roll-off is due to the UA or if the issue is the lack of points...
I have attached a plot of the low shelf frequency response. If you still want it I can give you the frequency response values for everything (high and low)... Do you want them in frequency linear or frequency log form? How many datapoints?
BTW, do not check to much the horizontal scale... it is tabulated for log-frequency.. there is a total of 100 point where the first point is 20Hz and the last one 20KHz
ruffrecords said:Thank you very much for taking the time to do this. As the information at the low end is suspect I suggest we concentrate on the high boost/cut curves. A log frequency and amplitude scales would be best for me for estimating turn over frequencies and slopes. I don't know if data points are spaced linearly or not but when I do a spice sim I usually set it for 20 points per octave. As 20Hz ro 20KHz is close to 10 octaves I guess 200 data points would be about right.
Once again, thanks very much for doing this. It is much appreciated.
Cheers
Ian
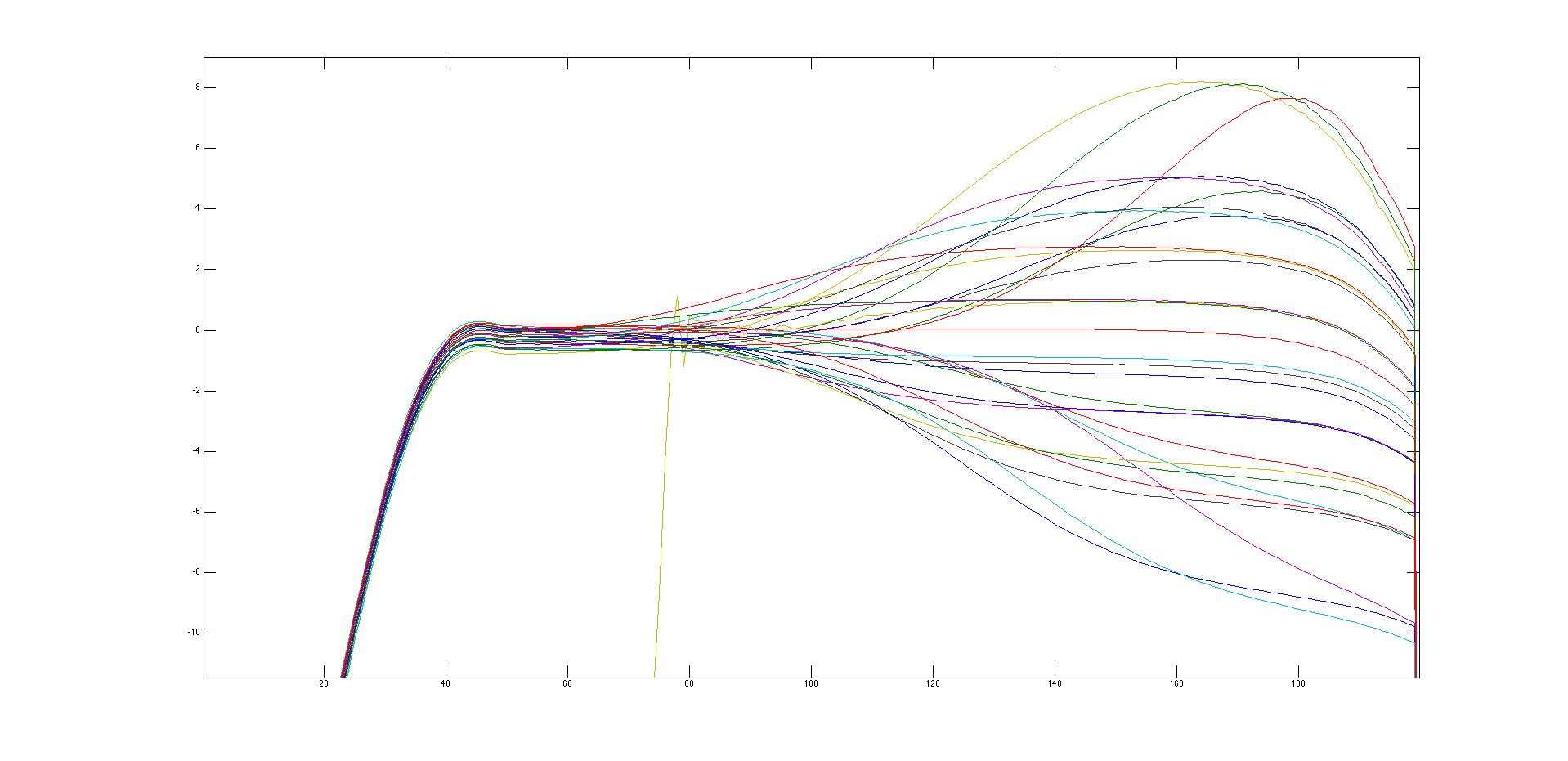
rickc said:I have a UA LA610-II and an Audio Precision System One. This is a combo of the UA610 preamp and an LA-2 compressor.
If it is helpful, I can run a family of curves for the equalizer.
Enter your email address to join: