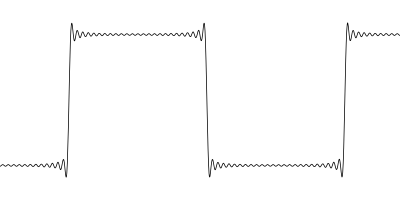
Rather than feed the veer already in process I thought I would start a new thread about square waves. People probably think they know what square waves are but details matter. Ideal square waves are defined as having instantaneous transitions from baseline to full scale, and back down again. Spoiler alert, nothing in nature is instantaneous. There are two popular ways to characterize fast moving waveforms; slew rate and rise time. Audio slew rates are generally defined as X volts per microsecond. Rise time is defined as time it takes for the waveform to rise from 10% to 90% of its max voltage also typically microseconds for audio circuitry.
More audio folk are familiar with slew rate as a performance metric routinely used to compare how fast op amps, or even audio power amps are. Rise time is more obscure and while comparing similar behaviors not widely embraced in audio equipment specifications.
To connect a few recently discussed topics (like NF and square waves) lets try to visualize what happens inside a typical op amp using NF when we input an ideal square wave. We have to use out imagination because ideal square waves don't exist in nature but some are fast enough for my purposes here. The instantaneous square wave transition up or down creates an input step error voltage because the output can't move instantaneously. This step error voltage will tell the op amp output to slew like a mother up or down. As the output starts catching up to the input signal the error voltage is reduced and the output rate of change slows creating the familiar curve as edge reaches level. This phenomenon has been awkwardly described as the amplifier "losing" NF during this catch up time. Different circuit designs behave somewhat differently which is why IC makers published square wave results.
Back in the 70s(?) some people tried to name new distortions based on this phenomenon. I was not a fan nor were some old school guys who cut their teeth designing HF radar technology during WWII. The new kind of distortion crowd wanted to anoint some winners and losers for their new distortion metric so used a square wave that was actually possible to make. They rise-time limited it through a LPF so it was difficult but not impossible.
Revisiting how typical op amp input stages respond to input steps (like square waves) there will immediately be a step error voltage between the + and - input pins that reflects how badly the output is not where the input says it should be. The dominant pole compensation stage is generally a simple one pole integrator. This integrators rate of change is a simple function of how big is the compensation cap, and how much current is the input LTP steering towards that integrator. The smaller the compensation cap the less current it takes to move it quickly. As long as this step error across the input stage is only a few mV the input LTP will remain linear (both devices conducting) and recover from transient events quickly. However if the error voltage step size if large enough to cut off the lagging LTP transistor it won't start conducting again smoothly. This is a bit of an oversimplification but explains the weirdness in some op amps recovering from (slew limiting) transients. Note: a simlar loss of NF occurs when outputs saturate into one rail or the other, this too can result in recovery related artifacts.
Back around the same time the one crowd was trying to invent new kinds of distortion, Dr. Marshall Leach (RIP) published a input topology that could not be slew limited. His design involved degenerating the input LTP with resistors such that a valid level input step signal (i.e. would not saturate the output stage) the overall response would be a well behaved rise time. (IIRC I linked to this Prof Leach AES paper here years ago, it was only a few pages long but iconic, IMO). Of course this "better" design created a conundrum for amplifier manufacturers who were saddled with customers who wanted to read slew rate specs with faster always being better. As I recall one manufacturer even had to footnote their amp data sheets with the reality that they defeated their rise time circuit to allow for data sheet slew rate measurements.
One thing I like about properly rise time limited signals a 1V square wave, and 10V square wave will look exactly the same only taller.
Mo later
JR
More audio folk are familiar with slew rate as a performance metric routinely used to compare how fast op amps, or even audio power amps are. Rise time is more obscure and while comparing similar behaviors not widely embraced in audio equipment specifications.
To connect a few recently discussed topics (like NF and square waves) lets try to visualize what happens inside a typical op amp using NF when we input an ideal square wave. We have to use out imagination because ideal square waves don't exist in nature but some are fast enough for my purposes here. The instantaneous square wave transition up or down creates an input step error voltage because the output can't move instantaneously. This step error voltage will tell the op amp output to slew like a mother up or down. As the output starts catching up to the input signal the error voltage is reduced and the output rate of change slows creating the familiar curve as edge reaches level. This phenomenon has been awkwardly described as the amplifier "losing" NF during this catch up time. Different circuit designs behave somewhat differently which is why IC makers published square wave results.
Back in the 70s(?) some people tried to name new distortions based on this phenomenon. I was not a fan nor were some old school guys who cut their teeth designing HF radar technology during WWII. The new kind of distortion crowd wanted to anoint some winners and losers for their new distortion metric so used a square wave that was actually possible to make. They rise-time limited it through a LPF so it was difficult but not impossible.
Revisiting how typical op amp input stages respond to input steps (like square waves) there will immediately be a step error voltage between the + and - input pins that reflects how badly the output is not where the input says it should be. The dominant pole compensation stage is generally a simple one pole integrator. This integrators rate of change is a simple function of how big is the compensation cap, and how much current is the input LTP steering towards that integrator. The smaller the compensation cap the less current it takes to move it quickly. As long as this step error across the input stage is only a few mV the input LTP will remain linear (both devices conducting) and recover from transient events quickly. However if the error voltage step size if large enough to cut off the lagging LTP transistor it won't start conducting again smoothly. This is a bit of an oversimplification but explains the weirdness in some op amps recovering from (slew limiting) transients. Note: a simlar loss of NF occurs when outputs saturate into one rail or the other, this too can result in recovery related artifacts.
Back around the same time the one crowd was trying to invent new kinds of distortion, Dr. Marshall Leach (RIP) published a input topology that could not be slew limited. His design involved degenerating the input LTP with resistors such that a valid level input step signal (i.e. would not saturate the output stage) the overall response would be a well behaved rise time. (IIRC I linked to this Prof Leach AES paper here years ago, it was only a few pages long but iconic, IMO). Of course this "better" design created a conundrum for amplifier manufacturers who were saddled with customers who wanted to read slew rate specs with faster always being better. As I recall one manufacturer even had to footnote their amp data sheets with the reality that they defeated their rise time circuit to allow for data sheet slew rate measurements.
One thing I like about properly rise time limited signals a 1V square wave, and 10V square wave will look exactly the same only taller.
Mo later
JR