Damping transformer ringing (Zobel network question)

[Val_r]

Hi,

Surfing the net trying to find some article on how to correctly damp transformer ringing, I came across this page.
I think it has some error in it: I tried to calculate the Ro, with no correspondence with the calculations in the text.
What's wrong?

The site cites the following textbook:
"Design Techniques for Preventing Input-Filter Oscillations in Switched-Mode Regulators",
Did anyone experienced it? Any link to a pdf?

Thanks.
:

 

[rodabod]

CJ quoted a text from Jensen here which explains exactly what you need to do.

 

[guavatone]

cope out a LF square wave while using a 20 to 100 pF cap and a 100K to 500K linear pot.  Adjust to taste while looking at the scope.  You want more square and less sine wave at the peaks.  measure value of pot then slap a resistor in there.

 

[skal1]

This ? had been  burning in the back of my mined for weeks ,glad Val_r had the guts to post it    ;D


regards

skal1

 

[PRR]

IF the unloaded transformer rings....

A resistor across the secondary will kill the ring. Obviously a zero-ohm load WILL kill ringy voltage, but also signal. A value similar to nominal impedance usually reduces ring compared to open-circuit.

If nominal load resistor makes ring negligible, and you can accept nominal input impedance, you are done.

Very often we need a fairly heavy load to kill ring, yet want a "high impedance" input to minimize source loading.

Note that we only need that resistive load near ringing frequency, not midband or bass. We add a capacitor in series with the resistor, so the bass/midband are not loaded, and the high ringy is loaded. Start with an RC product an octave below the ringy. Both the ring-frequency and damping will change, so experiment.

The ringy winding has a top-boost. The RC network tends to give a top-droop. Keep a close eye on overall response.

Don't try to eliminate ring. A few cycles of 18KHz is not, by itself, A Problem.

 

[Conductor]

Jensen text:

"Thanks for contacting Jensen Transformers.
There is no simple way to calculate the series RC damping networks for
microphone input transformers. Interwinding capacitance is not important,
it is distributed capacitance within the windings that matters, and this is
not an easily measurable quantity. Also, the transformer needs to be damped
with all of the circuit stray capacitances and loads in place around the
transformer. This is especially true with tube circuit designs where the
"miller" capacitance of the first stage may be VERY significant. The
simplest way to determine the proper damping network for a microphone input
transformer is experimentally. The method is actually quite simple and
fast once that you have done it a couple of times and have gotten together
the proper kit of tools to make it easy.

SETUP:

1) Drive the microphone input with a squarewave generator that has a
source impedance of 150 Ohms. This value is approximately in the middle of
the range of source impedances common to most microphones. If you have a
special situation where the microphone is going to have a known, much lower
impedance (say 20 Ohms), use this impedance instead. Make sure that the
output signal from the generator has nice clean, fast edges with no overshoot.

2) Set the generator for a signal level of approximately 0.1 Volts peak to
peak and a frequency of approximately 5 to 10 kHz.

3) Power the microphone pre-amp and adjust the gain to a level about 10dB
below clipping. The level isn't real critical, just make sure that the
pre-amp is operating in a normal gain range and that it isn't clipping.

4) Connect an oscilloscope across the secondary of the input transformer
using a x10 low capacitance oscilloscope probe. You MUST use a x10 probe in
order to prevent adding SIGNIFICANT capacitance across the secondary of the
transformer. Make sure that you have "calibrated" the oscilloscope probe
trimmer capacitor before starting this procedure.

5) Connect a capacitor substitution box in series with a 20k or 50k pot
and place this network across the secondary of the transformer. You may
also want to include a 1k pot in series with the 20k pot as a "fine"
adjustment control. The capacitor substitution box should have a range of
100pF to about 10,000pF for typical microphone input transformers. Extra
capacitors can be added in parallel if you need larger values. Standard 10%
value increments (100pF, 120pF, 150pF etc.) should provide enough
resolution for even "fussy" tweaking.

6) Make sure that the basic impedance determining load resistor is in
place across the secondary of the transformer. This value is typically 1500
Ohms x the turns ratio squared (for example our JT-115K-E uses 1500 Ohms x
10 x 10 = 150kOhms). This resistor sets the input impedance of the
microphone pre-amp.

ADJUSTMENT PROCEDURE:

1) Set the capacitor substitution box to the highest value (1000pF to
10,000pF) and adjust the pot for maximum resistance value (20k to 50k).

2) While watching the oscilloscope, lower the value of the pot. This
should decrease the overshoot of the waveform and reduce the ringing.
Adjust the pot for the highest value that will prevent all the overshoot
and ringing.

3) The objective now is going to be to find the SMALLEST value of
capacitance and the HIGHEST value of resistance that will eliminate all the
overshoot and ringing and leave just a smooth, flat topped squarewave with
a nice fast rising edge.

4) Keep decreasing the value of the capacitance and re-tuning the pot
until you can no longer eliminate the ringing and overshoot by adjusting
the pot. Go back to the last higher value of capacitance and do a final
tweak of the pot and then measure the final resistance value. These values
are your final damping network.

NOTE: Some transformers will have very high frequency, very small amplitude
ringing in addition to the main lower frequency, large amplitude ringing.
You will probably NOT be able to tweak this effect out of the transformer,
but it is usually not anything to worry about because it is so far removed
from the audio frequency range and results in only a small fraction of a
dB of frequency response variation at a point where the transformer
response is already 10dB or 20dB down from reference level.

Dale Roche - Project Engineer "

 

[CJ]

i never fully understood the zobel, if you take the ring and shunt it to ground, the pri does not know  the difference, it is still wasted energy due to the leakage.

and the ringing will probably not affect anything except what a K-9 hears, maybe, maybe not.

let it ring, thats what i say. be proud of all the turns it takes to ring.

putting a cap in there can create all sorts of weird filter poles and stuff

or maybe i am being paranoid.

it is just that the zobel will not add frequency response, it will only stabilize the ring.

 

[emrr]

I'm with CJ a bit.  All my transformer preamps are antiques, and there's not a zobel among them.  I've yet to measure response and find an untamed boost on the top; all have well behaved upper roll-off curves. 

Modern iron seems to need them in many cases, where old iron does not.  The Cinemag 600:50K input sounds pretty wacky with mismatched source Z, for instance, and the fixed Z load seems to be specified. 

I have definitely encountered people who think a zobel messes with the sound.  I can't vouch for the validity of that statement, but there is a dissenting view. 

Nice to see an official statement on method. 

 

[1954U1]

All my transformer preamps are antiques, and there's not a zobel among them.   I've yet to measure response and find an untamed boost on the top; all have well behaved upper roll-off curves. 
Modern iron seems to need them in many cases, where old iron does not. 

I've seen this diff too, on my old and new transformers,
Whats the reason??

 

[xmvlk]

there's not a zobel among them. 

Oh yes, old school.
Taming of the resonance of the transformer can be done by three ways:
input resistance
output resistance (sink 50 kOhm)
zobel (R+C)
or
both three.
In the old textbooks (i.e Cykin, Transformatory nizkoj czastoty, russian 1950 book)
only theoretical formulas for computing input and output R taming are given (and formullas are pretty)
Problem is, that output resistance, needed for optimal damping, is too low and give some
gain reduction in the middle frequency band.
Zobel network gives no gain reduction in the mids, but it is hard to get analytically.
But problem is, that if you have analytical formulla to compute Zobel exactly
(I do mean, that there is a way to get it from complete modell of transformer),
where you get complete transformer model with all leak inductances, parasitic capacitances
and how the model wary in your partiucular preamp. (i.e. parasitic capacity which see the transformer
varies a lot in every PCB configuration, maybe twice).
It is better to tune up Zobel in your equipment when the transformer see the real parasitics.

 

[xmvlk]

Whats the reason??

Maybe, that output sink R resonance taming
also makes bass rollof lower. The paralel (self) inductance
of the transformer sees lower resistance.
(Of course on the cost of mid frequency attenuation)

 

[Val_r]

Hi guys,

Thank you all for the replies.
The Jensen text seems really interesting for an experimental and definitive solution, thank you conductor for posting it!

I am still curious about the theory of finding the mathematical model for the LC tank and tame it.

Let me clarify that I'm taming an output transformer.
It has the 620 ohms resistor on the secondary winding, it is a 4:1, so prim. is 10K.
I am posting pics of a 10KHz squarewave without the zobel and with the zobel (24 ohms in series with 15nF).
Here you are....

Hope it makes sense.
Any opinion, suggestion, comment more than welcome.

Respect,
Val

 

[rodabod]

What's the transformer?

Looks like you've solved the main ringing successfully, but there is still a main point of over-shoot (looks like quite a low harmonic). You always have to compromise though.

I would follow-up your test with a basic frequency response test too.

 

[Steve Hogan]

The Jensen text seems really interesting for an experimental and definitive solution, thank you conductor for posting it!

I am still curious about the theory of finding the mathematical model for the LC tank and tame it.

Let me clarify that I'm taming an output transformer.
It has the 620 ohms resistor on the secondary winding, it is a 4:1, so prim. is 10K.
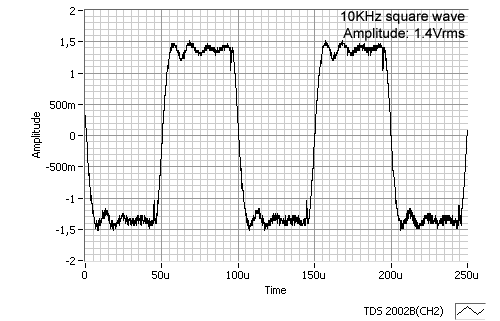
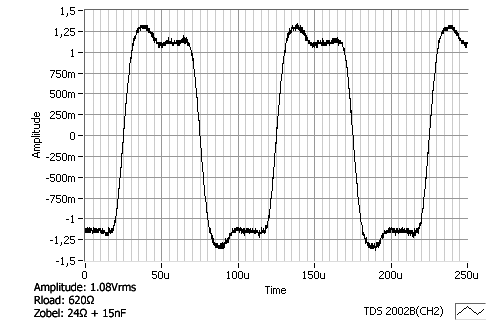
I am posting pics of a 10KHz squarewave without the zobel and with the zobel (24 ohms in series with 15nF).
Here you are....

Although it may be an interesting mental math skill exercise (sort of like solving a crossword puzzle), one cannot calculate the required RC network without all the parameters including strays included.  After you do all the exacting measurements that are required to derive the values for the model, and then do all the math, you will still need to adjust the values of the R and C in the lab for optimal response.

Dale's procedure spelled out in the Jensen document is very close to my own.  When I designed the JT-xx series of tranformers at Jensen, I had to determine hundreds of optimal RC damping networks. What Dale didn't explain is that we really didn't use a capacitor substitution box.  We had a kludge board with an air-core variable capacitor -like those used to tune in old-time vacuum-tube radios. This makes a variable capacitor of maye 50 pF to 500 pF which covers a pretty wide range of values. We switched in fixed caps in parallel to make bigger values.  In series with the variable capacitor(s) were 3 pots connected in series -- A 100k, 10k and a 1K in order to fine tune any value from 0 Ohms to 111kOhm.

It is important that you watch the square wave on the scope while you diddle the values -- a lot like playing a video game. You adjust both R and C for the fastest risetime and sharpest corner with no overshoot and ringing.
If the transformer has more than one resonance, you may not be able to get them all damped.  You can try two different networks in parallel, but really you should get a different transformer.  Transformers with more than one resonant frequency generally never sound as good as one, because every musical transient excites both resonances and the resulting intermodulation distortion generates very ugly and non-musically related sum and difference frequencies.  I had to work really hard to design out any multiple frequency resonances in my Jensen transformer designs.

Once you get a good looking square wave, measure the capacitance with a C meter and solder in the closest 5%standard value.  Then use the variable resistor(s) to re-tweak the network for best response with that capacitor. Since 1% resistors come in much finer steps than caps, you can usually get a standard value resistor that gives really good results.  Finally sub in a real resistor which will have less strays than a pot and make sure the square waves still looks great.

The scope photos that you show are of a problem transformer.  The 620 Ohm load resistor has already tamed the major resonance. Note that the only ringing left is at about 100 kHz and it looks like a secondary resonance to me.

The second photo shows an incorrect RC network  Your capacitor is too big. Your resistor is too small. The single low-frequency bump is your capacitor resonating the transformer leakage inductance and making it overshoot. The resistor is too low so instead of the network acting like an additional resistive load that kicks in only at HF, it is allowing the big C to be in parallel with the secondary thus resonating the transformer.  You have reduced the HF bandwidth and made a big peak in the HF response.  I predict that this particular transformer will sound better without your network.  You may be able to find one that works, but the ringing frequency is really low and will probably be very hard to damp.  This is the kind of transformer I would have never allowed to become a final product, but I would have tweaked the insides of the transformer to fix the ringing.

If you really want a nightmare -- try putting a cap across the secondary that simulates cable capacitance -- say 33pf/foot x 100ft = 3300pF.  The overshoot you will get will be very frustrating as the cable C interacts with the relatively high leakage inductance.

Output transformers must have extraordinarily low leakage inductance to not be affected by cable capacitance. That's why Jensen output transformers are multi-filar construction which gives very low leakage inductance and resulting insensitivity to load and cable capacitance.
Using a resistive pad at the output of your transformer (assuming that the amplifier has the headroom) may allow you to isolate the secondary from cable capacitance and minimize the cable induced resonance.

Many of the "vintage" transformers had lower bandwidth than modern ones.  Also, the Miller capacitance of many vacuum tube circuits is there but not on the schematic.

Having the proper RC network on the secondary of a tranformer that requires it, is critical to the sound of the audio circuit that it is married to. The high frequency ringing, if passed on to the following amplifier stage will ask the amplifier to follow the high frequency garbage precisely, and the amplifier has little feedback and running out of slew rate at those frequencies.  The amplifier, as a result, ends up putting out significantly more ugly intermod distortion than it would if the HF ringing was passively damped before ever reaching the following amplifier.

 

[Steve Hogan]

i never fully understood the zobel, if you take the ring and shunt it to ground, the pri does not know  the difference, it is still wasted energy due to the leakage.

and the ringing will probably not affect anything except what a K-9 hears, maybe, maybe not.

let it ring, thats what i say. be proud of all the turns it takes to ring.

putting a cap in there can create all sorts of weird filter poles and stuff

or maybe i am being paranoid.

it is just that the zobel will not add frequency response, it will only stabilize the ring.

With a scope you can see ringing on the primary of transformer with a badly ringing secondary.
The ringing has a huge effect on the intermodulation distortion of the amplifier that follows the transformer, so the circuit will sound much more smeared in the midrange if the transformer is allowed to ring.

The transformer itself is filled with built-in filter poles and stuff.  The RC network is just on the outside of the can.

A proper RC network can shape the HF response to a Bessel shape which will typically reduce the undamped peaking bandwidth.  The reduced deviation from linear phase and reduced intermod from the following stage makes for a much smoother, cleaner, and subjectively more extended high end, however.  Most folks find the sonic improvement is well worth the effort to find and install the optimum RC (Zoebel) network.

 

[emrr]

Thank you Steve.  Very well stated. 

 

[1954U1]

Thank you Steve.  Very well stated. 

Yes, very useful and in deep explanation!
I'd put it in the meta..

 

[PRR]

I'm not smart like Steve; but I like to leverage my ignorance.

> I'm taming an output transformer. It has the 620 ohms resistor on the secondary ... the zobel (24 ohms in series with 15nF)

It is supposed to be a 600 ohm load? Then 24 ohms in the Zobel is suspiciously small. And 0.015uFd against 600 is within the audio range (~~17KHz).

Look at the levels. Eye-ball averaging the bumps: the basic Square is 1.4V before, 1.1V after. Some brute-force is happening. Midband loss comes with the technique, but this is enough to warrant further study.

And as Steve points out: the simple-load ring is ~~100KHz. Do you care? If you do, can you lose it in a later stage? If this is an input tranny, the next tube/transistor does not need the extra work. If you drive 1000m of typical cable, you won't find much 100KHz at the far end. If you are driving loudspeaker, who cares tenth-volt 100KHz? However if you put NFB around this transformer, supersonic rings screw your stability and leave the amp working too hard.

Foo on the ringing. What is the Frequency Response? Steve says, and I suspect, it won't be great with that large cap hanging on the secondary. I had too much coffee. My hand jitters. Cna't tpye good. Gluing 5 pounds of mass on my palm reduces the jitter. Dose not imporve my typing.

I'd start with R=600. Or since we already know this is a problem-child, maybe 200. But it does not seem to make sense to go to "zero", which is what 24 is compared to 600. You are actually fighting the ~~40 ohm winding resistance, which "ought" to be "nearly negligible".

And try to keep C not far below nominal impedance at the top of the audio band; no 5 pound added mass. 0.015u is enough to hurt my typing and your cymbals and string-screech.

As Steve and xmvlk hint, source impedance matters. Are you driving the 10K with a 100 ohm source, or a tube plate, or ? ? ? It does make a difference. Some of the Jensen mike-input data and notes mentions that 200-ohm dynamics and 20-ohm active condensers favor different treatment or design.

I still don't think, in the field (rather than Steve's bench), there CAN be an "optimum". It gets down to making the best of what you have for -your- uses.

When you do good you can tune to a Bessel, with smooth amplitude and lovely phase and fair tolerance.... but when not doing so good a Bessel slopes the top of the band enough to hear. In desperation we turn to a Butterworth, which can be mighty flat up to a point (a more or less ringy point) and then fades 12dB/8ve. And phase will be curly well before the corner. But phase in the studio is always squirrelly, most listeners don't notice phase as much as top-loss. Sometimes a Butter-bump gets the job done. And when really pressed, sometimes you go to a Butter-BUMP, and apply a high-cut elsewhere in the chain. I've done that to get audio through "servo" transformers. I was not proud. In particular because it was load-sensitive.

You can tune a single ring. When a winding system is so distributed-parameter that you have multiple resonances, it becomes a mess only an Expert can wade across, and Steve says he'd rather find a different swamp.

 

[emrr]

I had too much coffee. My hand jitters. Cna't tpye good. Gluing 5 pounds of mass on my palm reduces the jitter. Dose not imporve my typing.

Excellent analogy. 

What is this transformer, and in what circuit condition? 

 

[Val_r]

Hi folks,

Thanks for the replies.
Please ignore the previous photos. They are not correct measurements.
After reading Steve's posts, I started to play tweaking Rloads of both input and output transformers, with 2 pots as suggested in the article.
Well, the correct value of termination resistor is fundamental.
The whole response of the entire circuit path is much much better.
The frequency response of the circuit is 10Hz -20KHz within -0.5dB.
Neither the input transformer (a Sowter 4383) nor the output xfm have a zobel, only the experimentally found termination resistor.
And this is what I get (Signal generator output at 50 ohms):

The sowter Rload is 10K, out xfm Rload=1.8K

Sowter really didn't like the 68K termination that I used before, and that is responsible for the bad resonance of the first pic snap.
I also played with output Rload, and the 1.8K is the best result, again with no zobel at all.
The output transformer is driven by a 12BH7 White Cathode follower, followed by two 4.7uF polypropylene caps in parallel.
Rk is 330 ohms, and about 13mA flow through it.

Open to comments....

Respect,
Val