DSP Whodunnit.

[chmedly]

Cut to Chase:
This is kind of a black box situation.  I’m trying to decipher the filter commands going to a dsp from a computer based interface.  I want to be able to emulate the computer and send my own commands to the box. 

The Long of It:
Here’s what I know.  The DSP chip is a Sharc ADSP21161. 
I’m 98% sure that the sampling rate is 48Khz and the bit depth 24bit.
Each filter command to the unit is comprised of 200 hex characters (100bytes).
Each command applies to 3 of what I’m calling “banks”. 
Each bank can hold an EQ filter. 
The filter options include:
Parametric -> Bandwidth, Frequency and Boost/Cut
Low Shelving -> 6db or 12db per octave, Frequency and Boost/Cut
High Shelving -> 6db or 12db per octave, Frequency and Boost/Cut
Low pass -> 6db or 12db per octave, response: Butterworth or Bessel
High pass -> 6db or 12db per octave, response: Butterworth or Bessel
Bandpass -> Bandwidth and Frequency
Frequencies are counted in 5hz increments.  Boost and Cut are in 1db increments.

Example command for High shelf 5Khz 12db/oct +1db written to the 2nd bank:
9659E23D0000803F32D6533EFD5D643FBCBB11BF2EE54B3F8CCC1A3FE4B9A43EEFFC0B3E073D8EBFFB61B53D77F
E7E3F9EC4B83EFB8370BF2B051DBFEB7F57BF19300A3F00000000000000000000030201008813F304353F000000000
000000000000000

Mystery 1:

The last 32 bytes are apparently intended to be written to the DSP for the purpose of being read back at a later time by the computer so it knows what filters are loaded.  The first 10 bytes (of these last 32 bytes) are for bank 1. The next 10 bytes for bank 2 etc.  The last 2 bytes appear to be padding as they don’t change always sitting at 0000.  What I’ve been able to decode of this is shown in this graphic.  The first byte indicates which filter type (parametric, high pass etc).  The first mystery is how to decode the frequency.  I haven’t been able to decipher if it’s simply a number conversion thing or if the frequencies are actually written into a table and this simply represents the index of that table.  5Khz = 008813, 100Hz = 006400, 500Hz = 00F401, 1Khz = 00E803

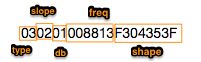
Mystery 2:

The 4 bytes immediately following the frequency indicate the response shape of the filter.  Any filters that don’t have a response shape show F304353F for this data which appears to correspond with Butterworth shape.  A Bessel response (for a High pass) is 0000003F.  And Bandwidth of 3.99 for a parametric filter is 8988883E.  Not sure what these numbers equate to. 

Mystery 3: The big one!

I assume that the first 68 bytes (leading up to the 3 banks at the end) are comprised of filter coefficients.  But instead of a set of coefficients for each bank it looks like all the values* change no matter if it’s changing one bank or all of them.  If I put a particular filter into the first bank it will produce the same 68 bytes that it does if putting the same filter into bank 2 or 3.  But only if that is the only filter (the other banks are empty).  If I populate 2 banks with filters then the 68 bytes don’t match.  The 68 bytes define a combined response for all 3 banks together.  If I put a high pass in bank 1 and a low pass in bank 2 and then swap the 2 filters such that the high pass is in bank 2 and the low pass in bank 1, the 68 bytes for the 2 different configurations are identical. 

*[The first 3 bytes are different for each different set of filters but the 3 bytes following appear to change only subtly depending on if a filter has a corner frequency below a certain frequency.  3A0000 if the frequency is below 35Hz.  3B0000 between 35Hz and 125Hz.  3C0000 between 130Hz and 585Hz.  3D0000 above 590Hz till around 7Khz.  Everything after that is different for each different filter or set of filters.] 

I recognize that there are a lot of different filter implementations and this might be a needle in a haystack but I’m hoping that “textbook” filters are at play here and once a few things a figured out the rest will fall into place.  Being a beginner with DSP coefficients I’m hoping to at least learn from this process.  So, anyone “recognize” any faces here?  Perhaps there is a Sharc filter tool that was used to develop this and it’s clear where the scheme came from? 

More examples:

bank 1 = High shelf 12db/oct 5Khz +1db
bank 2 = High shelf 12db/oct 5Khz +3db
126BBC3D0000803FB4621D3E39388E3F221382BE6E755D3FDC6B003F39EF8E3E1114683F9D229EBF4ED4D43EA4D5
683FA844F33E62F88ABF68BE93BF8ABB37BFCA43323F030201008813F304353F030203008813F304353F0000000000
00000000000000

bank 1 = High pass filter 100hz, 6db/oct butterworth:
755DCE3B000000001F03A83E12A95F3F54CAF8BE7BAB5C3FADC5013FC44BAA3EB9A98E3BFBFD7FBF96AA0EBBD8F
F7F3FA777AA3E738D5DBF354200BFF7C65DBFB6BDFF3E050100006400F304353F0000000000000000000000000000
0000000000000000

 

[efinque]

I think the last digits are something known as the carry bit (I've read about it somewhere, digital electronics books refer to it as LSB which stands for least significant bit)

Other than that it looks very low level. If you want to give own parameters to the chip using hex I highly doubt there's a viable solution to do so via physical controls without a MCU.

 

[chmedly]

Communication with the box isn't a problem.  Maybe I should be more clear.  I'm replacing the manufacturer control software for this box with my own.  And that side is actually already worked out.  Decoding the EQ is the last big hurdle that I've been saving for a big finale.  ;D

As far as carry flags go, I'm not sure that it makes sense in this context but I'm still thinking about it. 

Thanks for the input! 

 

[efinque]

Communication with the box isn't a problem.  Maybe I should be more clear.  I'm replacing the manufacturer control software for this box with my own.  And that side is actually already worked out.  Decoding the EQ is the last big hurdle that I've been saving for a big finale.  ;D

As far as carry flags go, I'm not sure that it makes sense in this context but I'm still thinking about it. 

Thanks for the input!

I don't know... I've been (edit : very recently) looking into DSP programming in C/C++ using Arduino Uno but I'm a noob at programming plus the board analog inputs are 10bit and the CPU is 8 bit.

EDIT : I've also been working on a crossover in Reaktor..

There are a few design flaws though..

There's basically a frequency lookup table for musical notes that feeds the subharmonic synthesizer (a sine wave oscillator) which doesn't suit "live" music really because the notes coming from the tracker will be "clean" regardless of the program material being in or out of tune in contrast to a real-time frequency tracking subharmonic synthesizer . I've yet to test it but it works really well on headphones for EDM.

EDIT 2 : The subharmonics part is also posted on NI forum.

 

[JohnRoberts]

If the dsp interface is proprietary, the extra bits could be anything... IIRC some early peavey DSP (1980s) used external gain scaling to maintain SN.

JR

 

[chmedly]

If the dsp interface is proprietary, the extra bits could be anything...

JR

So this looks like a needle in a haystack? 


I've been thinking and have realized that my first post was a huge data dump.  I apologize.

Let me restructure this into 3 questions:

1)  What kinds of digital filters can define (3) 2nd order filters at one time? 

2)  What kinds of digital filters might benefit from an "adjustment" for low corner frequencies?

3) Of these filters, which are most likely to be deployed on a floating point DSP like a Sharc? 

 

[efinque]

So this looks like a needle in a haystack? 


I've been thinking and have realized that my first post was a huge data dump.  I apologize.

Let me restructure this into 3 questions:

1)  What kinds of digital filters can define (3) 2nd order filters at one time? 

2)  What kinds of digital filters might benefit from an "adjustment" for low corner frequencies?

3) Of these filters, which are most likely to be deployed on a floating point DSP like a Sharc?

Hmm.. I've tried programming a 1-pole (edit : low-pass) filter in Reaktor from scratch and at it's core it was based on multiplying the signal somehow but I didn't get the module working for some reason.

EDIT : It looks like this..

I can't be bothered to fix it since there are a number of preset modules in the library.

 

[mskeete]

So this looks like a needle in a haystack? 


I've been thinking and have realized that my first post was a huge data dump.  I apologize.

Let me restructure this into 3 questions:

1)  What kinds of digital filters can define (3) 2nd order filters at one time? 

2)  What kinds of digital filters might benefit from an "adjustment" for low corner frequencies?

3) Of these filters, which are most likely to be deployed on a floating point DSP like a Sharc?

I like puzzles like this

Based on my limited DSP knowledge and SigmaDSP...

1) 3 X BiQuad IIR filters or one long FIR filter
The PC software could be calculating the overall response for all 3 banks and generating one set of coefficients for a FIR  filter.

2) below a certain frequency is best to use double precision. That could be whats going on here.

3) based on your observations i'm leaning towards an FIR  filter.

The numbers you're seeing for the frequency seem to be in LSB order.
They make more sense if you reverse the byte order

100Hz = 006400 -> 006400
500Hz = 00F401 -> 01F400
1Khz  = 00E803 -> 038E00
5Khz  = 008813 -> 138800

Based on that. 2Khz should be 07D000 or 00D007 as you'll see it.

Some more playing around with a calculator and
Hex value = Frequency (in Hertz) * 256 -> reverse byte order

The shape is probably Q or bandwidth.
Not sure how to convert those numbers yet - need more examples

 

[abbey road d enfer]

You need help from Alan Turing...

 

[efinque]

I like puzzles like this

Based on my limited DSP knowledge and SigmaDSP...

1) 3 X BiQuad IIR filters or one long FIR filter
The PC software could be calculating the overall response for all 3 banks and generating one set of coefficients for a FIR  filter.

2) below a certain frequency is best to use double precision. That could be whats going on here.

3) based on your observations i'm leaning towards an FIR  filter.

The numbers you're seeing for the frequency seem to be in LSB order.
They make more sense if you reverse the byte order

100Hz = 006400 -> 006400
500Hz = 00F401 -> 01F400
1Khz  = 00E803 -> 038E00
5Khz  = 008813 -> 138800

Based on that. 2Khz should be 07D000 or 00D007 as you'll see it.

Some more playing around with a calculator and
Hex value = Frequency (in Hertz) * 256 -> reverse byte order

The shape is probably Q or bandwidth.
Not sure how to convert those numbers yet - need more examples

I remember reading on speakerplans about the FIR vs IIR.

 

[abbey road d enfer]

I remember reading on blah-blah...

This link has nothing to do with the actual subject.

 

[chmedly]

Aha!  You figured out the frequency thing.  Here’s an example of another 1st order high pass.  Flipping the bytes around and then dividing by 256 seems to line up perfectly.  004001

Highpass filter 320hz, 6db/oct butterworth:
6770983C000000002DF3A23E5924633F5A13E9BE91765A3F1D74053FEB7DA93E9520633C87EB
7FBF8F2EE3BB6DFE7F3FE107AA3E68385DBFD5D200BFD2F05DBF4F2CFF3E050100004001F304
353F00000000000000000000000000000000000000000000

I like puzzles like this

Ok then, here's another data dump.  ;D

Here’s a parametric band.  With the HEX flipped around it’s 03F700.  Converted to decimal and then divided by 256 = 1015
parametric 1.015Khz bandwidth 1.89 -4db:
ADF6003D0000803FF0474F3EEA88573F0FDB91BD993D743F2D65993E23A4C03E0A999A3E472
B72BF6B28803EBDD9773F0F99C73E3A324FBFE12A16BFA65751BF6159133F0000000000000000
00000102FC00F703F304353F000000000000000000000000

I was coming to similar conclusions.  The two ideas I’ve had are either the software is plotting the response of the 3 filters together and then calculating FIR coefficients for that response or… the Analog Devices DSP “book” talks about combining IIR filters (either cascaded or parallel) into one set of coefficients using the Z-Transform.  I haven’t yet found a calculator for doing that and I’m not quite to the point where doing it “by hand” would make sense. 

I thought the FIR thing was kind of brilliant because it would probably allow the visual plot that is created in the software actually match what the box is really doing and it seemed like a good way to ensure that the latency through the filter was consistent no matter what filters were used.  What didn't add up was  A) If it was changing the number of taps used depending on the need for better low frequency accuracy, wouldn’t that be changing the latency?  B) Can you actually fit enough FIR coefficients to do this into the 68 bytes that are available?  C) If I understand correctly, the floating point DSP is probably more advantageous with double precision IIR filters.  D) Offering only Butterworth and Bessel filter shapes doesn’t quite line up with FIR filters.  Etc etc. 

My next step instead was going to be to wrack my brain to find a way that the coefficients for a simple IIR could be sorted out of the string of HEX.  Then I would know that it was indeed IIR and also where the coefficients were stored.  I’m wondering if the first 8 bytes might somehow represent poles and zeros.  I’ve noticed that if the filters are Low Pass or High Shelving then bytes 5-8 are always 0000803F.  If the filters are High Pass or Low Shelving then bytes 5-8 are, I think, either 0529643F or 00000000.  If the first 8 bytes are defining something like poles and zeros then what's left is 60 bytes for coefficients.  Assume 5 coefficients then there are 12 bytes per coefficient. 

Low Shelf 3Khz 6db/oct -1db:
9C94BE3D0529643F525A8B3EDA77463F07E216BF420E443F7E9D243FE07AA03E066734BDD1C
27EBF1AFA84BDB5757F3FA785A43E9F2E5FBFB67CFABE44FC5FBF74ECF73E0201FF00B80BF30
4353F00000000000000000000000000000000000000000000

bank 1 = Low shelf 12db/oct 5Khz +1db
bank 2 = Low shelf 12db/oct 500Hz +3db
bank 3 = Hi Pass 6db/oct butterworth 100Hz
CFEF9E3B00000000CA91093D0735AA3FA6E405BE8E867F3F233E793DFC017C3E6A85673F7432
1BBFCD565F3FC43EFA3E8528373F533CBFBEDE906DBF9C1BB5BE08736F3F020201008813F304
353F02020300F401F304353F050100006400F304353F0000

bank 1 = Low shelf 12db/oct 5Khz +1db
bank 2 = Low shelf 12db/oct 500Hz +3db
bank 3 = Low Pass 12db/oct butterworth 1Khz
44865D3CC8DDCA3FF84D033D1167AF3E026B8EBF322A7F3F884BA53DA1CC273E6F033CBE4F
2419BDE764733F89AF9E3EDF614A3FFA7295BADBFDB63B1C7F0E3E5C827D3F020201008813F3
04353F02020300F401F304353F04020000E803F304353F0000

Low Pass 300Hz 12db/oct Butterworth:
21BC543C0000803F465B483E321487BD3A3678BC081B7D3F4C8C193E509FC93E273D75B95322
2F3A68DE963E3BA2743F2C8DCB3E61EE073875C3C73797A54FBFA4BA153F040200002C01F304
353F00000000000000000000000000000000000000000000

Low Pass 300Hz 12db/oct bessel:
9357193C0000803F5C954F3E3D7E3BBDEA3C4ABC37107C3F7BE3323E6C60C83E534578B9C33
C2C3ADAE2933EAF16753F2A0ACB3EAD0507381659C737FFDD4FBF4C6C153F040200002C0100
00003F00000000000000000000000000000000000000000000

Lastly, I’ve found that byte 4 changes it’s frequency split points at different frequencies if the filter is 12db/oct as compared to 6db. 

 

[chmedly]

You need help from Alan Turing...

Do you have his email?
  :

 

[efinque]

Do you have his email?
  :

I believe the Turing machine doesn't have imap/pop capabilities.

 

[mskeete]

The gain in db seems to be stored in a single byte - 2 compliments so -4= FC
is it correct that the existing interface doesn't allow fractional db values - e..g 6.5dB?

if you take the "shape" parameter and reverse the byte order and convert to a IEEE754 32 bit float then you get
0000003F -> 3F000000 -> 0.5 = Q for a bessel filter
F304353F -> 3F3504F3 - 0.70710677= Q for a butterworth filter
8988883E -> 3E888899 -> 0.26666716 - nowhere close to 3.99 but close to 1/3.99.
What hex value do you get if you set the bandwidth to exactly 4.00?

What sample rate is this DSP using?

I'm going off the idea of FIR coefficients.

That frequency field might only be 4 hex digits instead of 6. That would make more sense as then you dont need the 256 factor.
Do you ever see no zero values for the first 2 bytes when you sweep through frequencies?

 

[efinque]

The gain in db seems to be stored in a single byte - 2 compliments so -4= FC
is it correct that the existing interface doesn't allow fractional db values - e..g 6.5dB?

I'm not an expert on the subject but for example a Driverack PX+ accepts only 0.5dB increments.

if you take the "shape" parameter and reverse the byte order and convert to a IEEE754 32 bit float then you get
0000003F -> 3F000000 -> 0.5 = Q for a bessel filter
F304353F -> 3F3504F3 - 0.70710677= Q for a butterworth filter
8988883E -> 3E888899 -> 0.26666716 - nowhere close to 3.99 but close to 1/3.99.
What hex value do you get if you set the bandwidth to exactly 4.00?

What sample rate is this DSP using?

I'm going off the idea of FIR coefficients.

That frequency field might only be 4 hex digits instead of 6. That would make more sense as then you dont need the 256 factor.
Do you ever see no zero values for the first 2 bytes when you sweep through frequencies?

There's a module (=some lines of code) in Reaktor called DNC which stands for denormal cancel. I've only recently looked at chips such as the UAF42 which have a selectable filter type by input pin but in general hex code readings don't really tell much about what they do as the ASICs/FPGAs and other ICs are either configured in the factory which is when you'll have a hard time figuring it out or by the user which is when you should know what you're doing.

 

[chmedly]

The gain in db seems to be stored in a single byte - 2 compliments so -4= FC
is it correct that the existing interface doesn't allow fractional db values - e..g 6.5dB?

FYI some of these questions were answered in my first post.  Not that a forum post is the easiest way to disseminate (or remember )this kind of info.  But yes, this unit uses 1db increments universally.  A bit coarse but functional. 

if you take the "shape" parameter and reverse the byte order and convert to a IEEE754 32 bit float then you get
0000003F -> 3F000000 -> 0.5 = Q for a bessel filter
F304353F -> 3F3504F3 - 0.70710677= Q for a butterworth filter
8988883E -> 3E888899 -> 0.26666716 - nowhere close to 3.99 but close to 1/3.99.
What hex value do you get if you set the bandwidth to exactly 4.00?

If I set it to 4.00 then the UI automatically changes it to 3.99.  I’ll see if I can get some more bandwidth examples.  But if bandwidth is 1/Q then this makes sense? 

What sample rate is this DSP using?

I’m pretty sure it’s 48Khz.  All the info points to this but I don’t think I have an easy way to absolutely confirm.  The UI offers no control of sample rate and there are no digital ins or outs.  (Well, except a proprietary one). 

I'm going off the idea of FIR coefficients.

That frequency field might only be 4 hex digits instead of 6. That would make more sense as then you dont need the 256 factor.
Do you ever see no zero values for the first 2 bytes when you sweep through frequencies?

Good catch.  I can’t find an example where the byte directly after the gain (db) is not 00.  I initially assumed it part of the frequency field because the db byte would only need to be one byte. 


Lastly, I forgot to include this previously.  This is the command that disables all 3 filters. 

No filters:
2549123E0000803F2549923E079D1F3F1C2648BF079D1F3F1C26483F2549923E87DC63BEE0947
9BF87DC63BEE094793F2549923EE5A566BF0226DEBEE5A566BF0226DE3E00000000000000000
00000000000000000000000000000000000000000000000

 

[chmedly]

Ok, so I've realized some of my naivety about filters.  In a previous post I mentioned the Poles and Zeros.  Well, the filter coefficients ARE the Poles and Zeros.  I had the impression that there were some ways to define aspects of the Poles and Zeros besides defining their values.  I'm still not sure if this is the case. 

Anyway, in an effort to parse out the hex as potential coefficients, I wrote a little python script that breaks a long string of hex into 4 byte increments and then converts to IEEE754 32 bit float.  I've tried plugging various bits of these into the filter grapher at earlevel.com but none of the responses seem to be making sense yet.  Well, except that the coefficients are all between -1 and +1 in value which seems to imply FIR. 

Attached is the python script.  It should run on 2.7 or 3.  Anyone who wants to try it can simply download the file and then rename it to <HEX_TO_FLOAT.py>  (.py isn't a supported file format on this forum)  If you want to read the script you can open the txt file in a text editor.  To run it you simply need to open it with your python interpreter.  Usually this means typing in a command line:  <python HEX_TO_FLOAT.py>  from the directory where the file is.  Type "exit" to quit the program. 

 

[mskeete]

I really should learn python. I went off the language as soon as I read that white space / layout matters
I was going to write a script in Perl (showing my age) to parse the hex.

I have some code / spreadsheets that generate coefficients for biquad filters. for a lot of the filter types, two of the coefficients are the same. not seeing that here in your data.

Do you mind stating what system it is that your trying to reverse engineer?
if you have access to the hardware, there's probably going to be a crystal near the DSP IC or convertors which will help with sample rate.

Going back to the bandwidth - if you cant chose 4.00 then chose some "nice" numbers like 0.5 / 1.0 / 2.0

 

[chmedly]

I really should learn python. I went off the language as soon as I read that white space / layout matters
I was going to write a script in Perl (showing my age) to parse the hex.

I would recommend that you throw some time at it.  It's pretty easy and there are a lot of resources on the interwebs these days.  Layout does matter in terms of indentation but I don't find it to be off-putting.  There is a theory that if you are running out of room from indentation, you're doing it wrong. 

I have some code / spreadsheets that generate coefficients for biquad filters. for a lot of the filter types, two of the coefficients are the same. not seeing that here in your data.

I AM seeing identical coefficients.  I've been focussing on the numbers for the "No Filters" state and, well, here they are. 

0.142857149243
1.0
0.285714298487
0.623489797115
-0.781831502914
0.623489797115
0.781831502914
0.285714298487
-0.222520932555
-0.974927902222
-0.222520932555
0.974927902222
0.285714298487
-0.900968849659
-0.433883726597
-0.900968849659
0.433883726597

The fact that the 2nd one is a "1.0" looks like an IIR with that one being the first pole.  But I haven't found a way that this graphs to flat magnitude and phase.  It seems like I'm really close to getting this.  There are probably a couple simple things that I'm missing. 

Another thought: If we disregard the first 2, this list looks like it can easily be broken into 3 sets of 5 coefficients which would correlate with 3 second order biquads.  But this doesn't exactly jive with the way it appears to merge the responses of the 3 filters.  Again, I think I'm  just missing something that should/will be obvious.  Or I'm assuming something I shouldn't. 

Do you mind stating what system it is that your trying to reverse engineer?

I suppose there's no point in any mystery any more (I figured a black box might make it more intriguing.)
This is for Lectrosonics DM series.

if you have access to the hardware, there's probably going to be a crystal near the DSP IC or convertors which will help with sample rate.

The crystal is 12.288 which strongly suggests 48Khz.  12288/256 = 48

Going back to the bandwidth - if you cant chose 4.00 then chose some "nice" numbers like 0.5 / 1.0 / 2.0

I'll have to set up another jig (the computer at my other desk is already set up) but these numbers are "bandwidth" so I'm not sure how nice they're going to be.  http://www.rane.com/note170.html
It's been my understanding that many manufacturers do not follow the same logic and therefore have different calculations between Q and bandwidth.  For instance, Bessel Q should be closer to .577.  Perhaps in this case when they say "Bessel" they just mean a much gentler knee than Butterworth?