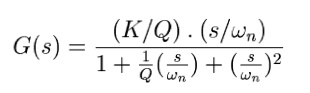Matador
Well-known member
I've been studying the following schematic:

I've been trying to ascertain the design equations for the parametric midrange portion of the control. I have some design equations for the Baxandall bass and treble sections but have been struggling with the circuit analysis for the topology around IC1B.
What I'm interested in is:
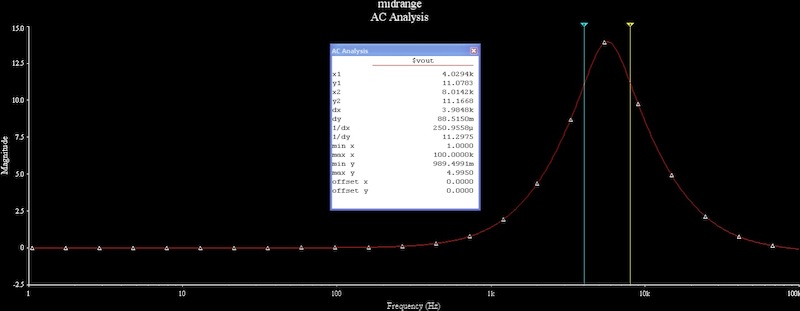
1) Frequency points for the poles and zeroes that define the bandpass region (I assume the equations should contain two poles and two zeroes to define the pass band).
2) Maximum gain at the mid center frequency
3) Q of the filter
4) Gain outside the pass band
So let's assume for analysis purposes that R11 is dialed to the top (maximum boost), and that R10 is dialed fully 'down' (so that R10 disappears from consideration for the moment).
The (roughly) equivalent circuit is this (omitting the effect of R11 for the moment):
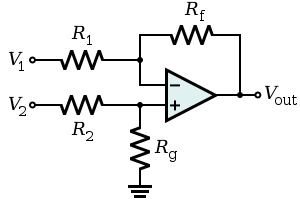
With V1 = V2, R1 = R8, Rf = R9, and the complex impedance of R12 and C5 being equal to R2, and the complex impedance of R13 and C6 being equal to Rg.
So question #4 above is the easy one. At DC, C5 and C6 are open, which means the non-inverting input is tied to ground through R13. At 'high' frequencies (f >> the pass band), the non-inverting input is grounded through the short that is C6. In either case, the circuit reduces to a standard inverting stage with R8 and R9 defining the gain of the stage. So if we want 0dB gain (unity) outside of the pass band, then R8 must equal R9.
Doing the nodal analysis of the differential amplifier yields the following equation for the gain:
VOUT/VIN = - (Z1*Zg - Zf*Z2)/(Z1*(Z2+Zg))
I think this result is correct as I see a similar equation posted in textbooks for this topology.
Here is where it get's nasty. If I let Z2 = (R12 + 1/s*C5), and Zg = R13/(1+s*R13*C6), I get this simplification for the transfer function in the Laplace domain:
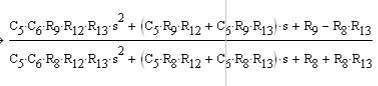
And here is the solution for the poles:
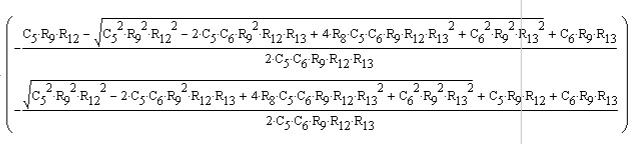
So the brute force mathematical approach yields complicated answers, but my gut tells me the overall approach should be easier. Just by inspection, the combination of R12 and C5 should form a zero, and the combination of R13 and C6 should form a pole. Just plugging in the numbers, I get a -3db point for the zero and -3db point for the pole that match the simulation exactly. So the two turn frequencies are:
f1 = 1/(2*PI*R12*C5)
f2 = 1/(2*PI*R13*C6)
Center frequency should be (using geometric mean principle):
SQRT(f1 * f2)
which again matches the simulations exactly.
Is there an easier way to go about this without pre-guessing the final answer?

I've been trying to ascertain the design equations for the parametric midrange portion of the control. I have some design equations for the Baxandall bass and treble sections but have been struggling with the circuit analysis for the topology around IC1B.
What I'm interested in is:
1) Frequency points for the poles and zeroes that define the bandpass region (I assume the equations should contain two poles and two zeroes to define the pass band).
2) Maximum gain at the mid center frequency
3) Q of the filter
4) Gain outside the pass band
So let's assume for analysis purposes that R11 is dialed to the top (maximum boost), and that R10 is dialed fully 'down' (so that R10 disappears from consideration for the moment).
The (roughly) equivalent circuit is this (omitting the effect of R11 for the moment):

With V1 = V2, R1 = R8, Rf = R9, and the complex impedance of R12 and C5 being equal to R2, and the complex impedance of R13 and C6 being equal to Rg.
So question #4 above is the easy one. At DC, C5 and C6 are open, which means the non-inverting input is tied to ground through R13. At 'high' frequencies (f >> the pass band), the non-inverting input is grounded through the short that is C6. In either case, the circuit reduces to a standard inverting stage with R8 and R9 defining the gain of the stage. So if we want 0dB gain (unity) outside of the pass band, then R8 must equal R9.
Doing the nodal analysis of the differential amplifier yields the following equation for the gain:
VOUT/VIN = - (Z1*Zg - Zf*Z2)/(Z1*(Z2+Zg))
I think this result is correct as I see a similar equation posted in textbooks for this topology.
Here is where it get's nasty. If I let Z2 = (R12 + 1/s*C5), and Zg = R13/(1+s*R13*C6), I get this simplification for the transfer function in the Laplace domain:
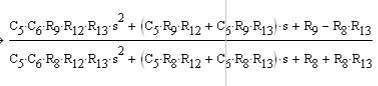
And here is the solution for the poles:
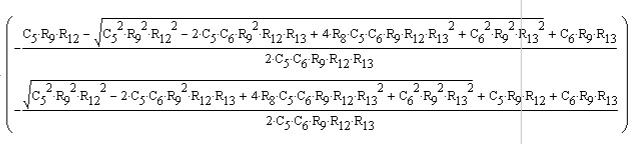
So the brute force mathematical approach yields complicated answers, but my gut tells me the overall approach should be easier. Just by inspection, the combination of R12 and C5 should form a zero, and the combination of R13 and C6 should form a pole. Just plugging in the numbers, I get a -3db point for the zero and -3db point for the pole that match the simulation exactly. So the two turn frequencies are:
f1 = 1/(2*PI*R12*C5)
f2 = 1/(2*PI*R13*C6)
Center frequency should be (using geometric mean principle):
SQRT(f1 * f2)
which again matches the simulations exactly.
Is there an easier way to go about this without pre-guessing the final answer?