Coil Winder

[CJ]

Back at it on the winder math. Figured out how to determine the angle that the wire would make with the bobbin as it relates to the distance that the feeder pulley is from the center of the bobbin.

Picking the right frame of reference and coordinate system can sometimes make a terible problem a lot easier. With trig, it's nice to have one or more boundries set up to equal either 0 or 1 if you can do it. Also, before I was going to do the math of the x axis only, negating any y axis motion, thinking that if the wire was far enough away from the bobbin that the effects can be ignored. This turned out to be less than realistic, as the wire will be close enough to the bobbin to feel the effecyts of y axis accelration. So now I am including y movement with the math. Two space is not too difficult, right? :shock:

This problem puts a square bobbin in a round circle, so we will probably be dealing with two coordinate systems. One for circular motion, and one for an X-Y cordinate system.

If you tape the magnet wire to the corner of the bobbin and pull on it, the bobbin will align itself. This alignment will put the corner of the bobbin on the x axis, along with the center of the bobbin, or the spindle of the winding machine, and the feeder pulley. This is how I set up all the problems.

In order to find the angle of the wire, I constructed a line segment perpindicular to the tanget line formed by the wire and the bobbin at the start of the winding cycle. Now, since we have a right triangle, we can solve for the angle by using the length of this perpindicular and the distance between the pulley and the center of the bobbin. For a square bobbin, the wind cycle will form a periodic function in the circular motion cordinate system that repeats itself every 90 degrees. The start of this function will depend on the size of the bobbin and the distance to the pulley. It took quite a while to find this hidden triangle needed to solve the problem. The crux of the solution lies in the fact that the perpindicular line segment pulls the tangent line into the correct frame of reference.

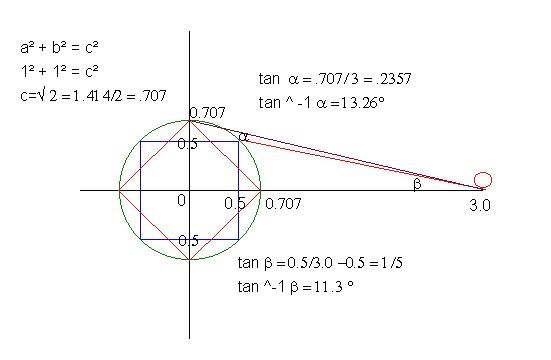
Here is a picture of the solution. You could do an extra step and use the two sides of the triangle to find a third, and then use the arc tangent method: ø = arctan L/√(D^2 - L^2)

Anyway, here is the pic. The triangle used can be transposed into a different quadrant in order to put the angle needed in the normal position. Note that as the bobbin fills up, the angle steepens. (PRR) Also, see that the radius of the circle that a square bobbin and wire travel in will be L x √2 .

You could use implicit differentiation in order to see what happens to the angle as the distance increases, or just look at the graph of an tangent function, or just realize that as you increase the distance to the bobbin, the angle tends rapidily toward zero.

 

[CJ]

I threw together a wire DIYreeler. Had to chop up one of my fishin poles, but the only thing I ever caught on it was a miniature Bluegill, so no biggy. You can see another fishin line guide on that rotor blade thingy. Do not know if it is ceramic or not. Probably plastic imitation, we will find out after 15 miles of wire have gone thru it.

http://vacuumbrain.com/The_Lab/Winder/tension1.jpg

So you have a mill, but no lathe? No problem! Just go down to the local supply house and score yourself a 6 dollar lathe bit and presto!

http://vacuumbrain.com/The_Lab/Winder/lathe1.jpg

I needed to step the drill rod in order to seat the sealed bearing.
The blade is 1/16 inch G-10 epoxied to the bearing:

http://vacuumbrain.com/The_Lab/Winder/tension2.jpg

Here it is in action on some #48. Works like a charm. The friction from the sealed bearing contamination barrier supplies enough tension. Plus wind resistance when it reallig gets spinning. I used it on some #50 also. You can see the rod tip a janglin round like I just got a hit from a 12 pound large mouth.

http://vacuumbrain.com/The_Lab/Winder/tension3.jpg

 

[PRR]

You are coming off the end of the spool? :shock: :shock: :shock:

That puts a twist in the wire.

I guess it is not an issue at this scale.

 

[CJ]

I think it depends on how they spooled it at the factory. In the old days, I believe the wire was unwound with the spool on a horizontal axis. Most of the stuff nowdays is meant to be taken off the end. If your lucky, you do not get any kinks. If you get a bad spool, you have to flip it over once in a while. If you wind fast enough, the centapetal force will unkink about anything.

 

[CJ]

More math, just a stall til some parts come in for this winder.

We found the angle for the start of a winding cycle based on the distance the wire feeder is from the bobbin. Now we are asking about the maximum height that the wire reaches during a winding cycle as related to the distance that the wire pulley is from the center of the bobbin. Still working with a square bobbin, so each cycle is the same, and lasts for 90 degrees.

The maximum elevation, or height that the wire will reach during a cycle, will be at the place where a tangent line from the pulley touches the circle:

Lets put some numbers down, so we can check our work as we go. Nice to actually use something learned in Math class in a real world situation.

Let's use a unit circle, radius equals 1, to make life easier. And we will say that the pulley is 3 units from the spindle.
To find the point of maximum wire heigth, we need to find the equation of that tangent that passes through (3,0) and touches the circle:

Well, there is always more than one way to solve a math problem, you can use different systems and translate axis, the first easy way I see to get information on this problem is to do the same thing we did to find the starting angle, drop a perpendicular, R, from the tangent line and use inverse sin to get the angle, solve for the rest of the coordinates, and you will have the answer.

For this particular problem, we will have the wire angle equal to
arc sin of 1/3 = arcsin 0.3333 = about 19.47 degrees.

So the internal angle in the circle to this perpendicular will be 90 - 19.47 = 70.53 degrees. Now we can find the highest elevation of the wire by finding the Y cordinate of 70.53 degrees, which is sin 70.53 = 0.9428.

We can subtract the starting height of the wire from this number to get the Δ Y for the wire, or the up and down distance it travels during a cycle.

We can check this geometrical solution against a solution that uses calculus in order to verify that we are not on crack.

This is a little tougher than the above method, so fasten your mathematical seatbelts!

Well, in the above drawing, we know that the tangent line we are after will pass thru the point (3,0). If we knew the slope of the line thru this point, we would have the equation of the line, based on the point slope form: (Y - Y¹) = m(X - X¹)

But what is the slope? Well, we can find the equation for the slope of any tanget to our circle by taking the first derivative of our equation for this circle. Since the point on the circle where the tangent hits is also a point on our tangent line that passes thru (3,0), we can solve a system of equations to get our answer.

But the equation of a circle can not be differentiated in the normal fashion, since we have a Y^2, not just Y. We can, however, differentiate implicitly:

X^2 + Y^2 = 1

So....

∂y/∂x (X^2 +Y^2) = ∂y/∂x (1)

2X + 2Y ∂y/∂x = 0 (power rule)

2Y ∂y/∂x = -2X , so

∂y/∂x = -X/Y .

So the slope of any tangent line to our circle at the point (X,Y) will be -X/Y.

We can now plug the equation for the slope into our line formula:

(Y - Y¹) = -X¹/Y¹(X - X¹)

multiply both sides by Y¹ to get rid of the denominator and we have:

Y¹(Y - Y¹) = -X¹(X - X¹) so we have

Y¹Y - Y¹^2 = -X¹X + X¹^2 grouping some terms...

X¹X + Y¹Y = X¹^2 + Y¹^2

See any substitutions we could do? Look at the right side of the equation? Remind you of anything?
.
.
.
Yes! The equation of a circle! So in our case, X¹^2 + Y¹^2 = 1. So sub in 1 for the right side of our equation, and we get:

X¹X + Y¹Y = 1

This is the general equation for any tangent line to our circle that passes thru the point (X¹,Y¹) . If we plug our (3,0) point, we can find the equation of the tangent line passing thru this point:

3X + 0Y = 1. So 3X = 1 which means X = 1/3. This is the X cordinate of the tangent where it touches the circle. Plugging this into our circle equation,

(1/3)^2 + Y¹^2 = 1

1/9 + Y¹^2 = 1

Y^2 = 1 - 1/9

Y^2 = 8/9

Y = +/- √(8/9)

Oh boy, it looks like we have two solutions for Y. Did I drop a sign somewhere?
But wait, thats OK, because if you look at the above pic, you see that there are two tangents to the circle passing thru the point (3,0), one on the top, and one on the bottom. The top one is the guy we want, so our cordinates are

(1/3, 2√2/3), or about (0.3333, 0.9428)

It's a miricle! Look at our newly found Y coordinate and compare it with the one we found with the geometrical solution.

Check the X value if it floats your boat.

We can find the slope of the line with our two points...

m = ΔY/ΔX = (2√2/3 - 0)/(1/3 - 3) = -√2/4

So, the equation of the line that represents the magnet wire as it reaches it's peak height for say, a bobbin that measures 1 inch from center to corner, and is being wound by a pulley 3 inches away will be

(Y - 0) = -√2/4(X - 3)

Y = -√2/4X + (3√2)/4

The max height of the wire above the X axis will be 0.9428 inches.
Notice that the tangent crosses the Y axis at about 1.060, so the max height is not at the top of the circle.

If you do some more math, you will also see that the max height is not reached at the halfway point of the winding cycle. Proof of this is left to the student as an exercise. :razz:

Next up: An equation for the wire using the Law of Cosines. Then we shall have a complete set of equations that describe the wire motion as it is wound on a square bobbin, which can help us to determine where to put the bloody lead screw, if it ever shows up!

Fun, isn't it?

 

[fernm]

Hi All

(I've been lurking for a while - this is my first post.).

I just though I'd post this link which may help on the math:
http://www.sciencenews.org/articles/20040403/mathtrek.asp

I'm not a mathematician at all, but I intiuit that there is something in the math of Reuleaux that could help.

Cheers and have a good holidays to those that observe.

Fernando

 

[CJ]

Than you Fernando and welcome to the forum!

Cool links, fits right in with this!
The second link is packed with stuff. Done by the same people who do the Mathematica software.

I did some plots on wire travel vs different distances for the wire feeder pulley. I set up the problem so that I am solving the triangle for the side that represents the wire distance from the point where it leaves the feeder pulley to the corner of the bobbin as it rotates:

http://vacuumbrain.com/The_Lab/Winder/wire_travel2.jpg

The colored line segments represent the wire length as the bobbin rotates 90 degrees through the winding cycle. Distance divided by time equals velocity. Since we are holding our revolution speed constant, the distance represented by the line segments can be thought to represent velocity.

I did a spreadsheet that uses the Law of Cosines formula. DIfferent pulley distances were used. A plot of the triangle side as it cycles though 1/4 revolution from a fixed pulley distance looks like this:

http://vacuumbrain.com/The_Lab/Winder/tgraph1.jpg

If we want to explore the change in velocity, acceleration, and all that good stuff, we can take the derivative of our Law of Cosines equation, or we can do another graph that plots the delta between the triangle segemnts, which is essentially what a derivative is. Here is a graph showing the change in the triangle side as we cycle through 1/4 revolution. Note that it is important to draw the graphs using the correct start and stop points in degrees. Luckily, we have figured this out in the earlier posts. For instance, if we are 2 units from the bobbin center, we use a cycle of rotation from 24 to 114 degrees. (114 = 24 +90) 24 was arrived at by dividing .707 by 2 and taking the arcsin, since we are using a unit circle where the distance to the bobbin corner from the center is 1 unit, and the tangent to the side has a perpindicular of 1/√2.

If we were four units away, we would use 35 to 125 degrees as our initial and final degrees of rotation.

Here is a graph done from the triangle side deltas.
We finally have what we we after. A way to plot wire accelrations as related to bobbin size and distance from the feeeder pulley.

This curve represents the deltas from the above column graph. The distance of the pulley is 2 units:

http://vacuumbrain.com/The_Lab/Winder/tgraph2.jpg

Here are some more plots. As you get further away from the bobbin, accelerations start to become more symetrical. It is interesting to note that for a fixed bobbin speed, the accelration of the wire changes depending on how far you wind from. The amount of wire being fed remains constant, but the rate that it comes off the spool will change, depending on the distance of the pulley.

Here is a graph of what the wire will be doing with the pulley right next to the bobbin:

http://vacuumbrain.com/The_Lab/Winder/tgraph3.jpg

Here are the plots for a pulley distance of 3 and 4 units respectively:

http://vacuumbrain.com/The_Lab/Winder/tgraph4.jpg

It is interesting to note that you get a more symetrical graph from a pulley distance of 2, it gets wacky at D=3, then mellows again from D=4 and there on out. This is exactly what I was looking for in order to know where to wind from. It also might be helpful if an attempt is made to use a stepper for a bobbin motor and trying to encode a program that will get rid of these non linearties in the winding cycle. I do not know if a winding machine exists that does this.

There is a place down the street that winds extremely fine coils using # 58 etc wire. They get used in hearing aids and surgical implants. They use a laser that tells them the angle that the wire is making with the bobbin, thereby eliminating a fixed rate method. This takes out all the varience in wire diameter as the coil is wound. Pretty sneaky. The laser must be aligned with the wire somehow.

Happy Holidays!

cj

 

[Larrchild]

energize the wire with some rf and pass it along a plate that forms the other half of a capacitor. As the angle changes, so will the capacitance=) use that to control the feed. Theremin-style

A few pf of change at a high enough freq could make quite repeatable results. Or using inductors on each side of the wire and make it pass between them. One could get an exact analog waveform of the error signal for the motor.

or jam a magnet in each high point on the side of the bobbin and use a magnetic position sensor like this:

" 103SR analog position sensors detect the proximity of an external magnet and produce a linear output. It comes in a rugged sealed, threaded aluminum housing." Based on the magnets sweeping by, it would create something like 4 of your D=4 curves per rev, but not true feedback for the slack problem like the capacitance would be though.

http://catalog.sensing.honeywell.com/vsg_compare.asp?FAM=solidstateSG&ITEMLIST=873043,873044,873047,873048



I found these techniques :


Linear Position Sensors and Switches, Variable Reluctance (9 companies) Variable reluctance linear position sensors and switches are noncontact devices that use variable reluctance based technology, and whose output signal represents the distance between an object and a reference point.

Linear Position Sensors, Capacitive (23 companies) Capacitive linear position sensors are devices that sense position / displacement using capacitance technology.
.. so I can see they are already doing this.

 

[Jeremy H]

I'm very late to this discussion - but in the spirit of diy I wll share anyway.
A friend of mine makes lap steel guitars and he wanted to have a go at at making single coil pickups.

He came up with an old record turntable to do the winding. For counting the winds he used a stop watch - you know 33 1/3 winds a minute. Not very accurate but the home cooked pickups sounded good!!

 

[CJ]

This is a toughy:

∫ √ (5 - 4 cos x) ∂x

Anybody?

I smell an ellipse.

 

[Viitalahde]

Hey CJ, if you could use these sensors I have in your winder, be my quest, I'll send them to you.

Here's the old Black Market post:

http://www.groupdiy.com/index.php?topic=10817&highlight=allenbradley+sensors

 

[CJ]

Thanks Jaako! Thanks Larry! Will look into those thoughts. Proximity sw would be good to change traverse direction.

That simple integral is turning out to be quite the monster, which is alwas the way it is with integration.

Here is a cool integrator from Mathematica:

http://integrals.wolfram.com/index.jsp

Here's what I got from it:

http://vacuumbrain.com/The_Lab/Winder/d1_ellipitical.jpg

Or the general form:

http://vacuumbrain.com/The_Lab/Winder/ellipitical_general.gif


I was trying to integrate the velocity eq. of the wire in order to get a location function to graph. Turns out you need an ellipitical integral, which is a semi hard to understand section of mathematics. Started when someone tried to calculate the length of an ellipse curve.

This is the best Table of Integrals book you can buy:

Table of Integrals, Series, and Products, Sixth Edition
by I. S. Gradshteyn, I. M. Ryzhik,

http://www.mathtable.com/gr/

Ellipitical integration was a part ot proving Fermat's last theorem, which was solved not too long ago.

Karl Weierstrass, Jacobi, modular transformations, it's all good.




Now if someone could explain how to work that E operator, .......... :?:

 

[bcarso]

Actually Wiles and Taylor used elliptic curves, which are a much different animal than elliptic integrals (cool though they are).

 

[CJ]

Taylor series?

Maybe the E means this:

or

Cool graphs:

http://www-m2.ma.tum.de/~kladire/divulgata/bucavgl/bucavgl.html


OT: came across a good site for PAF humbuckers:

http://www.provide.net/~cfh/paf.html

Online install for adding elliptic integration to Excel:

http://research.et.byu.edu/llhwww/538/class.html

 

[bcarso]

[quote author="CJ"]Taylor series?

[/quote]

Brook Taylor, who offered the general method for constructing them in 1715, is the man behind the eponymous series.

Richard Taylor, a grad student at the time of the announcement of the Wiles FLT proof, helped Andrew Wiles after defects were discovered. The paper that the two published, which with Wiles's first, really clinched FLT, is titled "Ring Theoretic Properties of certain Hecke algebras." Both papers can be found here: http://math.stanford.edu/~lekheng/flt/index.html

They are not for the faint of heart :green: A friend of mine compared reading them to reading Finnegan's Wake, based on his degree of understanding.

 

[CJ]

Oh boy.
109 pages on that one article.
I saw those two guys on a documentary of the proof. Pretty cool show.
Thanks for the link!
cj

 

[CJ]

OK, I finally decided that putting a 200 dollar counter on a DIY winder was
missing the point, so I grabbed this old counter off my first hand winder.

It's electronic, so it does not know the difference between fwd and rev, it
will count a turn either way, but I hope I will not be unwinding many
turns. Only 4 digits, but thats enough. If I go over 9999, I can tally a
one and move one.
Plus, the extra digits being out of the way is nice.

Old 74 series and some perf, and we cool.

http://vacuumbrain.com/The_Lab/Winder/wind_b.jpg

I made the infrared beam interuptor from that aluminum
blade you see there, but at max rpm, (2500), the counter started
floating max hits, so there was no diff between 2000 rpm and 2500
rpm as far as the counter was concerned. So I made a better blade
which has more on and off time built in. It is made out of a surface
mount
spool, like you see there in white. I put some paint on there to block
more light just in case. I am not missing any hits now.
I would rather have a round piece of plastic spinning
round than a knife blade. Better balance for the motor, also.

Here is the picker upper thingy. All this stuff is at radio shack
if you are bored.

 

[Larrchild]

I just realized how the digital tape counter in a cassette deck or vcr would be perfect for this. Got the interrupter and everything.

 

[The Kid]

CJ, you still working on that equation thing? Why would velocity of the wire even be an issue? You only need to know the max height of the bobbin. According to your drawings, the bobbin will stay in one place (rotate about an axis) as will the wire feeder, so if the bobbin is a 1 inch square, then:

 

[The Kid]

Boy, that picture looks like crap! Well, anyway, I came up with 11.3 degrees min. and 13.3 degrees max. for a one inch square bobbin. The circle (arc travel) comes out to d= 1.414 with those dimensions, and assuming the wire feeder is 3 inches away from the bobbin center. :sam: